About 80 school districts in Texas implemented the Algebraic Reasoning course in the 2016-17 school year and used our textbook as a preadoption resource. The AR development team at Cosenza & Associates, LLC, received invaluable feedback from teachers and math leaders in those districts!
One of the comments we heard from teachers around the state was that even though Algebra 1 is a required prerequisite for Algebraic Reasoning, many students still need help with Algebra 1 skills. As well, many students who are enrolled in Algebraic Reasoning courses are studying to retake the Algebra 1 End-of-Course (EOC) exam as a part of their graduation requirements.
To that end, we got to work.
TEKS Companion Guides are available for Grades 3-8 and Algebra 1!
Algebra 1 Companion Guide
We developed the Algebra 1 Companion Guide to accompany the Algebraic Reasoning textbook. The guide is available exclusively in print and is an interactive consumable student guide. The order in which the mini-lessons appear complements the progression in the Algebraic Reasoning textbook. However, this guide could be used for any EOC preparation program.
Mini-lessons focus on the Algebra 1 TEKS. There is a mini-lesson and set of practice problems designed around a compact instructional plan with three components.
- The Tell Me More section contains a brief summary of the key ideas, concepts, and skills that are addressed in the target Algebra 1 TEKS for that mini-lesson.
- Stepped-out Examples show students how to solve a problem that is based on the target Algebra 1 TEKS. Example problems address the multiple components (and multiple representations) contained in each TEKS/SE.
- Practice problems consist of a blend of constructed response and multiple choice questions that use the language students may expect to see on the Algebra 1 End-of-Course test. When possible, practice problems use griddable response questions so that students obtain practice using the grid that they will see on the Algebra 1 End-of-Course test.
How Were the Mini-Lessons Created?
Every Algebra 1 TEKS/SE is addressed in the Algebra 1 Companion Guide. For some lessons, it is appropriate to bundle a few TEKS/SE’s together, as in the case of A.2E, A.2F, and A.2G, all of which address writing equations of parallel or perpendicular lines.
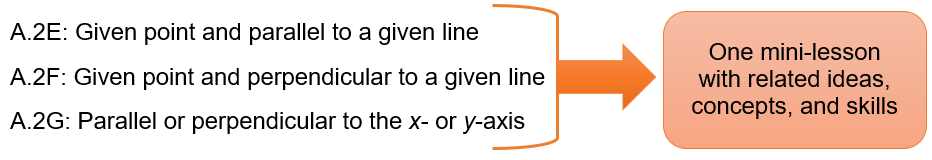
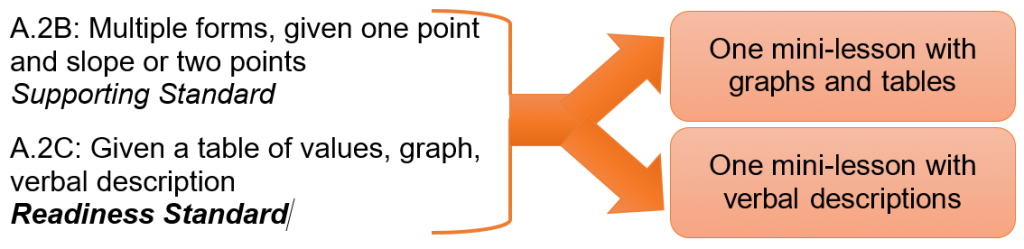
In other cases, one TEKS/SE or a pairing of TEKS/SE’s needs multiple lessons. For example, A.2B and A.2C pair nicely together and address writing linear equations from a graph, table of values, or verbal description. However, that pairing is too long for one mini-lesson, so the development team split the A.2B/A.2C pairing into two mini-lessons: one for writing equations from a verbal description and one for writing equations from a graph or table of values.
Teacher Manual
The Algebra 1 Companion Guide teacher manual contains an answer key as well as advice for how to use different features of the interactive student companion. The manual provides explanations connecting the Algebra 1 content to the information in the corresponding section of the Algebraic Reasoning textbook.
Pricing
The Guide, an interactive paperback consumable student edition, is sold individually with a minimum order of 20 student books. Pricing includes built-in volume discounts. One teacher manual is included for every 30 books purchased at no additional cost. ISBN: 978-0-9972265-7-7
- 20-30 student books are $20.99 each
- 31-60 student books are $17.99 each
- 61 or more student books are $14.99 each
Mini-Lesson Samples
View and download samples of the Algebra 1 Companion Guide mini-lessons! To open these in a new browser window or tab, please right-click and select Open Link in New Tab (Mac: Press COMMAND and click).
| TEKS | Sample Document |
|---|---|
| Grade 3 | |
| 3.3H: Comparing Fractions | View Sample |
| Grade 4 | |
| 4.7ABC: Measuring Angles | View Sample |
| Grade 5 | |
| 5.3H: Adding and Subtracting Fractions | View Sample |
| Grade 6 | |
| 6.4E: Ratios and Percents | View Sample |
| Grade 7 | |
| 7.4D: Solving Problems with Percents | View Sample |
| Grade 8 | |
| 8.4A: Slope as Unit Rate | View Sample |
| 8.8C: Solving One-Variable Equations | View Sample |
| Algebra 1 | |
| A.3C: Key Features of Linear Functions | View Sample |
| A.10B: Multiplying Polynomials | View Sample |
| Algebra 1 Errata Sheet | View Errata Sheet |
