The Texas State Board of Education’s Committee on Instruction met Thursday, November 19. One of their agenda items was an update on the implementation of the revised math TEKS. Hence, I was invited to testify about the mathematical process standards since that seemed to be the hot point in today’s hearing.
There were a few parents testifying with concerns about how the mathematical process standards seem to be interfering with the math that they feel their kids should be learning. One father expressed frustration with his child having to learn multiple strategies to perform basic computations with whole numbers, rather than “just multiplying the numbers” and moving on. Another parent was passionately concerned that her daughter suddenly didn’t like math anymore. I admire these parents’ courage for standing up for their children’s interests and feel proud that we have a governmental system in place that provides for parental input into educational decision-making. But if we peel back a few layers on this particular onion, we find out that there are some issues lying just beneath the surface that may be contributing to these observations.
What are mathematical processes?
We do know that mathematical processes are important. The National Council of Teachers of Mathematics (NCTM) published the Curriculum and Evaluation Standards in 1989 and first outlined important content and processes that every child should learn in math. The process standards that NCTM outlined were:
- Problem Solving
- Reasoning
- Representation
- Communication
- Connections
Some of the descendants of these five processes reside in both the original 1998 math TEKS and the revised 2012 math TEKS. These research-based mathematical processes help students make sense of important mathematics and help bring the strands of mathematical proficiency together. These are the thought processes that teachers can harness to help all of their students learn meaningful math.
What do they look like in daily instruction?
I was particularly moved by another parent’s testimony. He went right to the heart of the situation when he suggested, as many mathematics specialists have, that we use the visual models and conceptual pieces to lay the foundation and then bridge to the standard algorithm. To see what this means, let’s unpack the mathematical process standard 3.1E: create and use representations to organize, record, and communicate mathematical ideas, alongside content standard 3.4G: use strategies and algorithms, including the standard algorithm, to multiply a two-digit number by a one-digit number. Strategies may include mental math, partial products, and the commutative, associative, and distributive properties. To do that, let’s look at the multiplication problem 13 × 5 = 65.
You can use base-ten blocks to create a concrete representation of the problem. A ten-block, or rod (long) as it is called in the classroom, times 5 unit blocks generates 5 ten-blocks (rods or longs). 3 unit blocks times 5 unit blocks generates 15 unit blocks. These are grouped into 50 and 15, then combined into the product of 65.
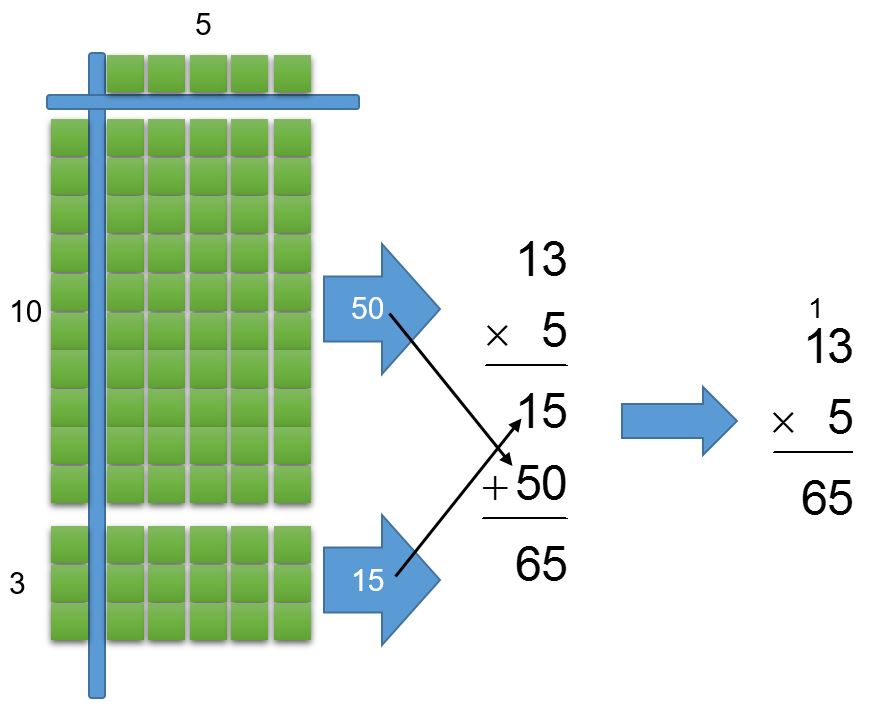
If you were to multiply 13 by 5 using a place-value based algorithm, you would line up the ones places and first multiply 5 ones by 3 ones. This generates the partial product of 15, which is the same partial product generated in the block model by multiplying 3 unit blocks by 5 unit blocks.
Likewise, you would next multiply 5 ones by 1 ten, generating the partial product of 50. This partial product is the same as the one generated in the block model by multiplying 1 ten-block (rod or long) by 5 unit blocks.
Notice how nicely the partial products approach segues to the standard algorithm for multiplying whole numbers. Multiply 5 ones by 3 ones, which gives you 15 ones. But you only have room for one digit, so you regroup 15 ones into 1 ten and 5 ones, record the 5 ones and carry the 1 ten to the tens column.
Next, you multiply 5 ones by 1 ten, which gives you 5 tens. Add back the 1 ten you carried over to get a total of 6 tens and you record 6 in the tens place of the product.
Yes, it is easier just to multiply 13 by 5 using the standard algorithm. That’s why we have the standard algorithm, which is much more efficient than using base-ten blocks or partial products. But each of these strategies helps students understand why the standard algorithm works. Using base-ten blocks provides students with a visual model of what it means to multiply 13 by 5. The model also shows students why the product appears in two parts: 15 and 50. The partial products help explain why we “carry the one.” These two strategies – base-ten blocks and partial products – lay the conceptual foundation for the important skill of using the standard algorithm to multiply numbers.
Without that conceptual understanding, anchored in place value, students get confused in 4th and 5th grade when they multiply 3-digit and 2-digit whole numbers and begin multiplying decimals. They’ll “carry the one” anywhere, dropping it where it feels like it fits. Investing time during 3rd grade to provide a solid conceptual foundation pays off in 4th and 5th grade because the student is more likely to extend what they know about multiplication to different types of numbers.
So what about November 19’s math TEKS hearing?
Timely question! We spent most of the math agenda item (#4 if you’re listening to the archived audio on the TEA website) discussing whether or not the mathematical process standards are helpful or harmful. When district-level curriculum frameworks and classroom-level instruction are wisely planned, the mathematical process standards are extraordinarily beneficial. By wisely planned, I mean that the teacher selects one process standard to showcase in the lesson, knowing that she is likely to address several mathematical processes in the flow of instruction. When planning with her grade-level team, they collaboratively select mathematical tasks that emphasize the showcase process standard while maintaining instructional focus on the content standard.
If a curriculum framework or instructional decision creates a situation such that every process standard should be applied to every portion (breakout) of a content standard, then the teacher gets lost in the weeds during instruction. That is not beneficial to students. I can also tell you as a member of a TEKS review/writing committee that this is certainly not the intent of the content/process standard pairing. Mathematical processes should be taught alongside the content standards to help students learn the full richness of mathematics. They become part of a student’s toolkit to think analytically and mathematically. Then, when a student encounters a problem they haven’t seen before, then they know how to wrap their heads around the problem and begin to look for a solution. That can only benefit students.
What’s the bottom line?
The mathematical process standards, either as they are used in instruction or assessment, should enhance student learning, not become a barrier to it. As educators, we should resist the temptation to let our fear of assessment lead us to irrational instructional decision-making. Process standards such as the use of multiple representations and creating representations to communicate mathematical ideas provide the teacher with guidance to select powerful mathematical tasks for her students. The mathematical process standards in the revised math TEKS are not new; indeed, they have been in the K-8 TEKS since 1998 in the “Underlying Tools and Processes” strand. As teachers, let’s use the mathematical process standards to our instructional advantage and our students’ benefit.
