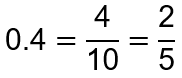To review the full Math-Grade 6 curriculum and see the online functionality, including ePub and assessment resources, please contact us to obtain login credentials.
The content that follows is what the teacher sees on the Lesson Overview page for each lesson in the teacher course.
Unit 1, Lesson 4: Equivalent Fractions, Decimals, and Percents
Lesson Overview
Focusing Question: How can I generate a fraction, decimal, or percent that is equivalent to a given number?
Learning Outcomes
- I can generate equivalent fractions, decimals, and percents.
- I can represent a rational number in a real-world context.
| Texas Essential Knowledge and Skills (TEKS) |
| 6.4G Proportionality. The student applies mathematical process standards to develop an understanding of proportional relationships in problem situations. The student is expected to generate equivalent forms of fractions, decimals, and percents using real-world problems, including problems that involve money. |
| 6.1A Mathematical process standards. The student uses mathematical processes to acquire and demonstrate mathematical understanding. The student is expected to apply mathematics to problems arising in everyday life, society, and the workplace. |
| English Language Proficiency Standards (ELPS) |
| 3.H Cross-curricular second language acquisition/speaking. The ELL speaks in a variety of modes for a variety of purposes with an awareness of different language registers (formal/informal) using vocabulary with increasing fluency and accuracy in language arts and all content areas. ELLs may be at the beginning, intermediate, advanced, or advanced high stage of English language acquisition in speaking. In order for the ELL to meet grade-level learning expectations across the foundation and enrichment curriculum, all instruction delivered in English must be linguistically accommodated (communicated, sequenced, and scaffolded) commensurate with the student’s level of English language proficiency. The student is expected to narrate, describe, and explain with increasing specificity and detail as more English is acquired. |
Overview of Process Standard(s)
In this lesson, students will use mathematics to represent problems that arise in everyday life, society, and/or the workplace. Students may:
- Use a fraction, decimal, and/or percent to represent a number in a scientific, financial, or everyday life context.
- Use information presented in a scientific, financial, or everyday life context to generate a fraction, decimal, or percent that represent the same quantity.
- Use a scientific, financial, or everyday life context to make sense of what a particular fraction, decimal, and/or percent means.
Prior Learning Supports
Percents are new to 6th grade math. However, students previously used visual models to represent equivalent fractions (Grade 3 and Grade 4) and related decimals to fractions (Grade 4). Percents were introduced in Grade 6, Unit 1 Lesson 1.
- 4.2G The student is expected to relate decimals to fractions that name tenths and hundredths.
- 4.3C The student is expected to determine if two given fractions are equivalent using a variety of methods.
- 4.3D The student is expected to compare two fractions with different numerators and different denominators and represent the comparison using the symbols >, =, or <.
- 3.3F The student is expected to represent equivalent fractions with denominators of 2, 3, 4, 6, and 8 using a variety of objects and pictorial models, including number lines.
In 3rd grade, students used number lines and pictorial models to represent equivalent fractions with denominators of 2, 3, 4, 6, and 8.
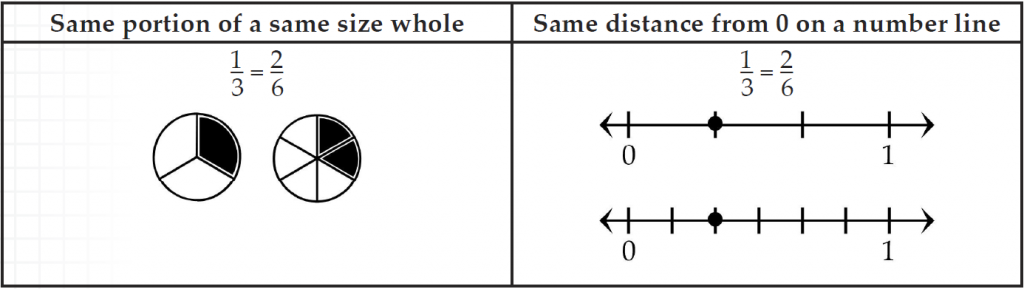
In 4th grade, students used a variety of methods (e.g., visual models such as area models or number lines) to determine if two fractions were equivalent. In an area model, if two fractions can be represented with the same portion of a same-size whole, they are equivalent. On a number line, if two fractions are the same distance from 0, then they are equivalent. Students also used symbols (less than, equal, or greater than) to compare two fractions.

Notably, 4th grade introduces students to multiple ways to represent the same quantity as either a fraction or a decimal. As students model tenths and hundredths, they name them as a fraction with a denominator of 10 or 100, respectively. Once the fraction is written, then students may generate an equivalent fraction. For example, four tenths can be represented in several ways.
Using visual models such as a hundreds grid to represent percents connects back to students’ experiences in 4th grade.
Lesson Plan
See the subsections below for lesson components and guidance for instruction.
- Exploration
- Play the instructional video to launch instruction.
- Guide students through the activity.
- Provide students with the Blackline Master of the Student Pages or assign the Google Slides as appropriate.
- Use the Answer Key as necessary.
- Explanation
- Assign students the ePub to provide direct instruction on the content along with guided practice through examples and a set of practice questions.
- Performance Task
- As a formative assessment, use the performance task to determine what students know about the topic.
- Performance tasks have four versions: on-level, simplified, enriched, and scaffolded.
- Allow students to work in pairs or small groups if desired.
- If there are multiple performance tasks, select one or encourage self differentiation by allowing students to select a task based on their interests and comfort levels.
Lesson Components
Pacing Guide
- Exploration (20-25 minutes)
- Explanation and Practice (20-25 minutes)
- Performance Task (30-35 minutes)
Teaching Hints
- Provide scaffolding tools such as number lines, hundreds grids, or fraction strips if students need additional support.
- For word problems, provide students with a problem solving model template as needed.
Teacher Materials
- None
Student Materials
- Pencil
- Paper
Vocabulary
One way to support students’ acquisition of new vocabulary terms is to preteach the vocabulary terms using a strategy such as a Frayer model. For these key terms, we provide partially completed Frayer models to which students should add as they move through the lesson and develop a deeper understanding of the vocabulary term. Click on the term to see the Frayer model. Use this template for additional vocabulary words.